路徑(Path)是指圖中的一個序列,其中連接相鄰節點的邊構成了一條路徑。路徑可以用來表示從一個節點到另一個節點的過程,並通常用來解決許多不同的問題,例如尋找兩個節點之間的路徑、檢測圖中是否存在特定類型的路徑等。
其中,最短路徑(Shortest Path)問題是圖論中一個常見的挑戰,其目標是找到圖中兩個節點之間的最短路徑。這個最短路徑可以按不同標準來衡量,如權重最小、權重最大、或者經過的邊或節點數最少等。
最長路徑問題是最短路徑問題的一個變體。在最長路徑問題中,你的目標是找到圖中兩個節點之間的最長路徑,而這個最長路徑是通過給每條邊的權重取負值來找到的。換句話說,最長路徑問題可以轉化為一個最短路徑問題,只需將所有邊的權重取相反數,然後使用最短路徑演算法來找到最短路徑,即可得到最長路徑。
以最短路徑問題為例,有幾種相關的演算法可供選擇,以應對不同情境:
這些演算法提供了不同的方法,可根據具體問題的性質和圖的特點來選擇適當的解決方案。最短路徑問題在路線規劃、網絡優化、通信網絡等領域有廣泛的應用。
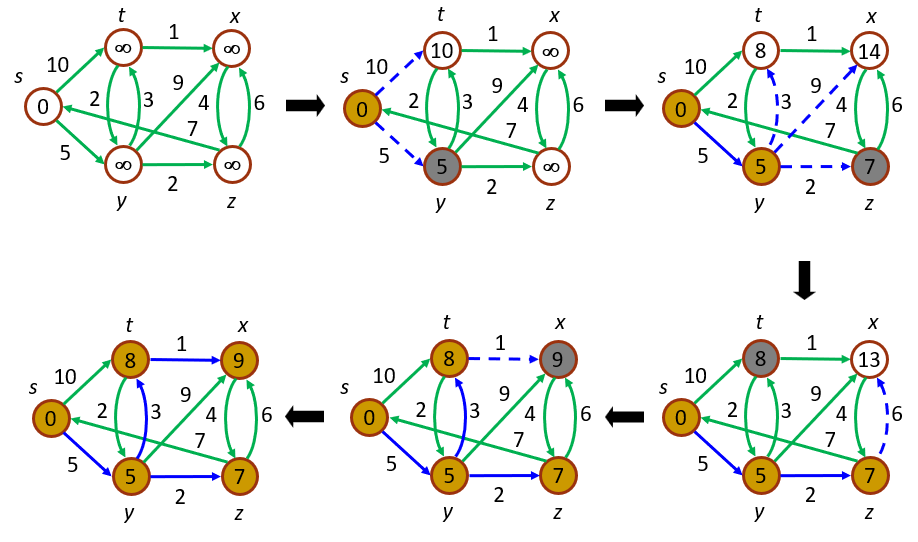
具體步驟如下:
const int INF = numeric_limits<int>::max();
class Graph {
private:
int vertices, edges; // 點的個數, 邊的個數
vector<vector<int>> adjMatrix; // 鄰接矩陣
vector<bool> visited; // 該點是否被訪問過
vector<int> distance; // 路徑長度
queue<pair<char,int >> shortPath; // 最短路徑
public:
Graph(int vertices) : vertices(vertices) {
edges = 0;
adjMatrix.resize(vertices);
for (int i = 0; i < vertices; i++) {
adjMatrix[i].resize(vertices, 0);
}
visited.resize(vertices, false);
distance.resize(vertices, INF); // 初始化距離為無限大
}
void addEdge(char from, char to, int weight) {
adjMatrix[from - 'A'][to - 'A'] = weight;
edges++;
}
int minKey() { // 找到最小權重的點
int min = INF, minIndex=-1;
for (int v = 0; v < vertices; v++) {
if (visited[v] == false && distance[v] < min) {
min = distance[v];
minIndex = v;
}
}
return minIndex;
}
void dijkstra(char start) {
distance[start - 'A'] = 0;
for (int i = 0; i < vertices ; i++) { // 次數
int u = minKey();// 找到最小權重的點
visited[u] = true;
shortPath.push(make_pair(u+'A',distance[u]));
for (int v = 0; v < vertices; v++) { // 更新最小權重的點的鄰接點
if (!visited[v]){ // 如果該點沒有被訪問過
// 新的路徑 < 舊的路徑 => 更新路徑
if(adjMatrix[u][v] && distance[u] + adjMatrix[u][v] < distance[v]){
distance[v] = distance[u] + adjMatrix[u][v];
}
}
}
}
}
void printShortPath(){
while(!shortPath.empty()){
cout << shortPath.front().first << ' ' << shortPath.front().second << endl;
shortPath.pop();
}
}
};
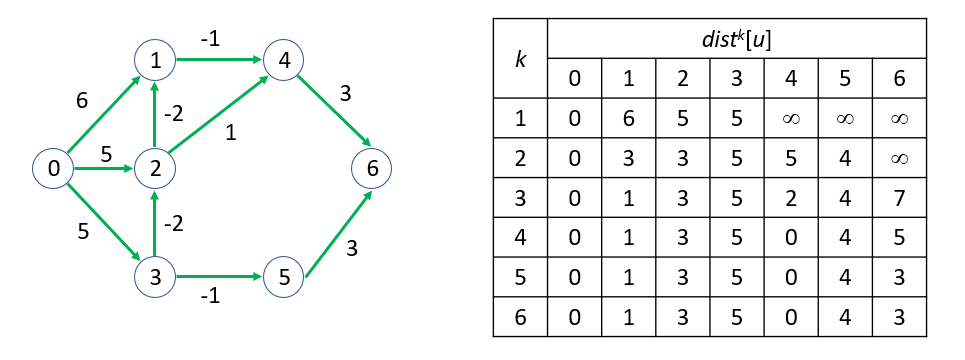
具體步驟如下:
const int INF = numeric_limits<int>::max();
class Graph { // 圖的結構
private :
int vertices, edges; // 點的個數, 邊的個數
vector<vector<pair<int,int>>> adjMatrix; // 鄰接矩陣 <點,權重>
vector<int> distance; // 路徑長度
public:
Graph(int vertices) : vertices(vertices) { // 初始化
edges = 0;
adjMatrix.resize(vertices);
distance.resize(vertices, INF); // 初始化距離為無限大
}
void addEdge(char from, char to, int weight) { // 加邊
adjMatrix[from - 'A'].push_back({to - 'A',weight});
edges++;
}
void printShortPath() { // 印出最短路徑
cout << "Shortest Path: " << endl;
for(int i = 0 ; i < vertices ; i++){
cout << char(i+'A') << ": " << distance[i] << endl;
}
}
void bellmanFord(char start){ //DP 演算法
distance[start - 'A'] = 0; // 起點的權重為0
// 遍歷所有點
for (int i = 0; i < vertices ; i++) { // 需要遍歷的次數為點的個數\
// 每次遍歷都會更新一次最短路徑
for(int u = 0 ; u < vertices ; u++){ // 遍歷所有點
for(auto v : adjMatrix[u]){ // 遍歷所有鄰接點
// 新的路徑 < 舊的路徑 => 更新路徑
if(distance[u] != INF ){
distance[v.first] = min(distance[v.first], distance[u] + v.second);
}
}
} // O(E)
} // O(V*E)
}
};
| 特性 | Dijkstra's Algorithm | Bellman-Ford Algorithm |
|---|---|---|
| 最短路徑類型 | 單一源最短路徑 | 單一源最短路徑 |
| 適用圖類型 | 無負權重邊,有向或無向 | 有向或無向,可含負權重邊 |
| 時間複雜度 | O(V^2) 或 O(Vlog(V)) | O(VE) |
| 優點 | 處理正權重邊快速 | 處理負權重邊 |
| 缺點 | 不適用負權重邊 | 較低效率 |
| 典型應用 | 網絡路由 | 金融建模 |
總結,Dijkstra's Algorithm適用於無負權重邊的單一源最短路徑問題,但不適用於負權重邊。Bellman-Ford Algorithm能處理帶負權重邊的單一源最短路徑,並檢測負權重環路,但效率較低。因此,選擇演算法應基於具體問題的要求和圖的特性。
每個人都有自己的節奏,不需要因為別人會的事情而勉強自己,也不必追求無止境的完美或頂尖。我們不必應付所有事情,也不必將所有知識都吸收。重要的是要了解自己需要的和想要的是什麼。
